

INDUCTANCE, CAPACITANCE AND RESISTANCE
Tip: print these pages out NOW! after loading
These are the principal passive components which make up most circuits we will discuss throughout these pages. A capacitor is a capacitor, an inductor is an inductor and of course a resistor is a resistor or an impedance at its rated value.
Don't you believe it because it ain't necessarily so.
We shall soon see that a capacitor can at certain frequencies look like an inductor and an inductor can look like a capacitor and our resistor may look a bit like both of them.
What is an Inductor
Well the letter L stands for inductance. The simplest inductor consists of a piece of wire. A piece of #22 wire which is approximately 100 mm ( 4" ) long has a measured inductance of 0.14 uH. Well mine did because I measured it on an inductance meter (see kits) operating at about 740 Khz. - [but compare that value with formula later].
Now this 100 mm length of conductor is about 25 mils (i.e. 25/1000") or 0.644 mm in diameter but does NOT carry rf throughout its whole cross-sectional area of 0.326 mm2. ( [Pi * Dia2] / 4 ) - another useful formula as you will soon see because I then use the traditional pi * r2 which is a pain if you talk ( as we mostly do ) in diameters.
At low frequencies this would be the case, but as the frequency is increased so is the magnetic field at the centre of the conductor and this leads to an increasing impedance to the charge carriers. This decreases the current density at the centre of the conductor and increases the current density around the perimeter of the conductor. We call this increase in current density around the perimeter "skin effect".
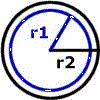 where
A1 = pi * r12
and A2 = pi * r22
where
A1 = pi * r12
and A2 = pi * r22
Skin depth area = A2 - A1
or
= [ pi * ( R2 2 - R1 2 ) ]
The net result of skin effect is a net decrease in the cross sectional area of the conductor and a consequent increase in the rf resistance. Consult the references I have suggested you read for a more detailed and informed discussion on this very important topic.
In particular I would recommend RF Circuit Design - Chris Bowick - Sams.
This skin effect we will see later on has a very significant impact on the Q of our inductors.
Throughout these tutorials I will incorporate as many relevant formulae as possible. Why?.
Because you will have under one roof all the formulae necessary to tackle any design goal you may have in mind.
Let's start out with the formula for the inductance for a straight piece of wire.
L = (.002 * length)[ 2.3 log {((4 * length)/dia) - 0.75}] uH
where:
L =
inductance in uH.
length = length in cm. (1" = 2.54 cm).
dia = diameter of the wire in cm also.
plugging in the details of our piece of wire which are, length = 10 and dia = 0.064, all dimensions being in cms.
L = (.002
* 4)[ 2.3 log {((4 * 4)/0.064) - 0.75}] uH
L = (.008)[ 2.3 log {((16 )/0.064) - 0.75}] uH
L = (.008)[ 2.3 log {249.25}] uH
L = (.008)[ 2.3 {2.3966}] = 0.044 uH
The reason I have included as many steps as possible is to help those people who do not necessarily feel comfortable with maths. Including as many steps as possible means they should be able to follow how we arrive at an answer. [now compare that answer with the measurement I made earlier???]
Now from the above equation you should begin to understand any piece of wire exhibits inductance. This of course includes capacitor and resistor leads as well as any inter-connecting wiring in your circuit. Circuit board traces exhibit inductance and in fact this property is often taken advantage of at UHF. We can draw inductors on the PCB's.
What if we decide to wind our 100 mm piece of wire into a coil? Here is another formula which is referred to as "Wheelers' Formula" - * Proc IRE, p 1,398, Oct 1928., although here the formula has been metricated. If you are more comfortable with imperial inches then delete the 0.394 and use inches in lieu of cm.
L = (0.394 * r2 * n2 ) / ( 9r + 10b ) uH
where:
L = inductance in uH.
r = radius of the coil (in cm).
n2
= number of turns in the coil squared and;
b = the length of the coil in cm.
Our length of 100 mm wire can easily become 2.5 turns wound on a 12.7 mm dia. former or even 5 turns wound on a 6.35 mm dia. former. If for convenience we make both coils equal in length to 12.7 mm then using the above formula and not forgetting to convert to cm and NOT confusing radius with diameter.
Time out for tirade -
I spent many years in the construction industry and cm is absolutely prohibitedas it should be everywhere else - unless you're a total idjut you can't mix up 1000 mm with 1000 metres but you can easily confuse 1000 mm with 1000 cm on a construction site. I have some recollection that at law, under the relevant original Metrication Act, cm is NOT officially recognized in Australia but is unhappily well beloved by retailers as well as my wife - boy we fight over that one.
End of unofficial tirade
Proceeding further you should have calculated inductances of (a) 0.054 uH and (b) 0.064 uH.
Our straight piece of wire has gone from 0.044 uH to 0.054 uH and 0.064 uH respectively.
A much flasher formula: (where coil length = diameter (which is best for optimum Q).
N = Ö[29L / 0.394r] OR L = [(0.394 * r * N2) / 29]
where:
N =
number of turns
L = inductance required in uH.
r = radius of the coil (in cm).
All others (29 & 0.394) are constants
Using example (a) above we would get:
L = [(0.394 * 0.635 * (2.5)2) / 29] = 0.054 uH
Permeability:- So far our inductors have been air wound where the permeability of air is 1. If we introduce iron or ferrites into our core then we find that for a given number of turns, the inductance will increase in proportion to the permeability of the core. This means for a given inductance less turns will be required.
e.g. Neosid have a fairly popular former (part 52-021-67 page 279) designed to accept a core of 4 mm dia. This former has an external diameter of 5.23 mm and a typical core at 20 metres (15 Mhz) would be an F29 type.
If we conveniently wanted an inductance of say, and of course I obviously cheated, 3.4937 uH and an F29 slug gives the formula:
N = 10.7 ÖL or N = 10.7 Ö 3.4937
we very conveniently get exactly 20 turns (remarkable wasn't it)
On the other hand to achieve the same inductance on a 5.23 mm former we would need to wind? Work it out.
Therefore introducing permeability means reduced turns therefore less rf resistance and hopefully greater Q.
Using the above former but with a different core and bobbin Mr. Neosid in his cattle-dog (australian for catalogue) page 264, tells me 150 turns of 3 x .06 EnCu wire, wave wound, will yield an inductance of about 670 uH. This would not be achievable without the permeability of core and bobbin, especially the claimed unloaded Q (Qu) of 150. Use the above formula and substitute a factor of 'X' for the 10.7 - what is the X?. If you need help, email me.
Toroids
These come in two types. Powdered Iron or Ferrites. Both introduce permeability. Toroids look exactly like doughnuts and come in various diameters, thicknesses, permeabilities and types depending upon the requency range of interest. Some of their advantages are:
· high inductance for the physical space occupied
· no interaction or coupling with adjacent components (unlike air wound and other inductors)
· various permeabilities available
· exceptional Q values when wound correctly and optimum core and windings selected
· wide range of diameters and thicknesses.
· relatively low cost
· often simple to mount or secure mechanically
The only disadvantage I can think of
· nearly impossible to introduce variable tuning of the inductance
Amidon Toroids available from - www.bytemark.com/amidon/
A typically popular type is made available by Amidon Associates and a representative example is the T50-2. This core is lacquered red (so you know the type) and has the following main properties.
Being T50 it's outside diameter is 0.5", the ID is 0.3" and the thickness is 0.19"
The permeabilities or in this case AL factors i.e. ( inductance per 100 turns2 ) for all T-50 types are:
|
TYPE |
COLOR |
AL |
Frequency Range |
|
T50-26 |
Yel-Wh |
320 uH |
power frequencies |
|
T50-3 |
Gray |
175 uH |
50 Khz to 500 Khz |
|
T50-1 |
Blue |
100 uH |
500 Khz to 5 Mhz |
|
T50-2 |
Red |
57 uH |
2 Mhz to 30 Mhz |
|
T50-6 |
Yellow |
47 uH |
10 to 50 Mhz |
|
T50-10 |
Black |
32 uH |
30 to 100 Mhz |
This is only a small sample to give you an idea. Your turns required to give a certain inductance based on the above AL is as follows:
N = 100 * Ö[ L / AL ]
Therefore to obtain an inductance of 3.685 uH using a T50-6 toroid would require 28 turns (of course I cheated again) but check it out on your calculator as I may have left in a deliberate mistake to see if you're awake.
By the way don't
get too paranoid about the exact number of turns because cores do
vary in value anyway and particularly with temperature changes.
Series or Parallel Inductors
Just as is the same with resistors, if two or more inductors are in a circuit connected in series, then the inductances add together, i.e. L total = L1 + L2 + Ln etc. If they are in parallel then they reduce to less then the lowest value in the set by the formula:
L total = {1/ [(1/L1) + (1/L2) + (1/Ln)]}
Enter all of those formulae along with every other one above and below into your exercise book.
Now for the downer:
I said in the second paragraph in the beginning that an Inductor can look like a capacitor.
What is a Capacitor
Well the letter C stands for capacitance. A capacitor is formed by two or more conductive parallel plates separated by an insulating material or dielectric. Typical dielectrics you will encounter are air, mica, ceramic or plastic.
Consider an air variable capacitor of the type used either as a trimmer or even the tuning element in a radio. It is merely two or more conductive plates separated by air - is this not so?.
Go back to our inductors above, could not a similar description apply to them?.
That is why inductors also have capacitance!. We have also learnt a small piece of wire has inductance. This is why capacitors with leads etc. exhibit inductance.
At some point our inductor with its inherent capacitance (called stray) will resonate (you will learn about that later) and this is called its self resonant frequency. The same rule applies to capacitors. Mostly it is only the VHF and UHF aficionado who has to be greatly concerned about these properties. Stray capacitance is everywhere. Sometimes it can be used to advantage, usually you take it into account (that is another function of trimmers) but often it's a monumental pain.
I said mostly - which means if you forget about it, then you can surely guarantee one day this property will bite you. That will be the day when you're working on your pet project, which of course won't work as expected and you don't know why your theory doesn't work out in the real world - another "gotcha".
Stray capacitance in sloppy layouts can account for unexpected oscillations, no oscillations, different circuit responses and generally cause you to "become a victim of the bottle, eternally caught in the grip of the grape and, if you become like me, occasionally ruin an otherwise good keyboard with an even much better claret - well actually 'Tyrrel's Pinot Noir' when the budget allows".
Even the best of designs and careful layouts are affected. Not only stray capacitance but stray inductance can affect you. Try some high speed, double sided, digital PCB designs.
Back to capacitors. Apart from their uses in resonant circuits they are used as:
(a) dc blocking devices - a capacitor will pass ac or rf but not dc. That is often the function of coupling capacitors in circuits. The coupling capacitor will pass our required signal but block the dc supply from the previous stage e.g. .001 uF (1000 pF or 1N0).
(b) supply by-pass capacitor - a capacitor used to pass ac or rf. Examples include by-pass of a dc supply to an emitter bypass capacitor. When used on a dc supply line the capacitor shunts (shorts) to ground any unwanted ac or rf to avoid contamination of our supply e.g. 0.1 uF (100,000 pF or 100N)
(c) reservoir by-pass capacitor - Used in the output of a dc rectifier to smooth out the power line ac pulses and as a reservoir between the charging pulses. Think of it as a big water storage tank. This is where you have the high value capacitors e.g. 10,000 uF / 63V. (10,000U)
(d) emitter by-pass capacitor - In the case of an emitter by-pass our transistor may, as one example, be considered as two distinct models. One under dc conditions which sets up how we want the transistor to operate and another under ac or rf conditions e.g. as an amplifier. In this case our emitter by-pass capacitor merely makes any emitter resistor invisible for ac or rf purposes typical values might range from 2.2 uF down to 0.1 uF. (2U2 down to 100N)
Parallel plate capacitors have a formula for calculating capacitance :
C = 0.22248 * K * (A/t)
where:
C = capacitance in pF
K = dielectric constant (Air = 1)
A = area of plates or dielectric in inches2
t = thickness of dielectric or spacing in the case of air variables.
Series or Parallel Capacitors: - Series and parallel combinations calculate in an opposite fashion to inductors, i.e. parallel = C1 + C2 + Cn and series are:
C total = {1/ [(1/C1) + (1/C2) + (1/Cn)]}
Now here come some very very useful formula. Using the one immediately above you should determine that a 22 pF capacitor in series with a 15 pF capacitor gives a total of 8.92 pF. Go ahead do it! check me out.
What if we had say 105 pF already in circuit and needed to reduce it to say 56 pF. A real world example might be say the only air variable capacitor available is one with a maximum of 105 pF. What do you put in series to reduce the maximum to 56 pF?.
Did you know the formula above, for two capacitors in series, can become:
C total = [( C1 * C2 ) / ( C1 + C2 )]**
AND:
C series = [( Cavail * Cwanted ) / ( Cavail - Cwanted )]
THEREFORE:
C series = [( 105 * 56 ) / ( 105 - 56 )] = 120 pF
If you disbelieve me then check it out using ** above as a double check. Nifty eh!. Write it in your exercise book. If that's flash try this red-hot formula.
Suppose we wanted an oscillator to tune from 7.0 Mhz to 7.2 Mhz. Now if you don't quite know what an oscillator is yet don't worry. For reasons we will explore later on in the tutorials you will find that your capacitance MUST vary, for tuning purposes, in the direct ratio of the frequency ratio squared or Cmax to Cmin = (Fhigh / Flow)2 . Eh What!.
In this example our frequency ratio is Fhigh / Flow = 7.2 / 7.0 = 1.02857. Our ratio must be squared so then it becomes (1.02857 * 1.02857) = 1.05796. This must be our capacitance ratio i.e. Cmax to Cmin = 1.05796.
Using the 105 pF air variable capacitor is no help because it usually has a minimum of 10.5 pF and that's a ratio of 10:1. Assuming the 105 pF, for the moment ***, is acceptable then apply this formula (which is quite difficult to do in HTML language the way I wanted to do it - so bear with me):
Cpad + 105 / Cpad + 10.5 = 1.05796 / 1
What needs to be done is re-write that formula on a piece of paper using two lines and writing the division sign in the usual way, i.e. as an underlining of both Cpad +105 and 1.05796. I hope everybody knows what I mean. Next we perform a simple algebraic function, we cross multiply so you should end up with:
Cpad + 105 = (1.05796 * Cpad ) + ( 1.05796 * 10.5)
Cpad + 105 = (1.05796 Cpad ) + ( 11.10858)
then subtracting 1 times Cpad from each side as well as subtracting 11.10858 from each side (in algebra what is done to one side of the equal sign must be done to the other side - I hope that's clear also) we get:
93.89142 = 0.05796 Cpad and dividing both sides by 0.05796
Cpad = 1619.93 pF
Now firstly I accept the fact that the formula may be obscure for many people and if that is the case then I will re-write it as a graphic but including too many graphics can cause other problems. It is MOST important (to me anyway) that I make this as easy as possible for you.
Secondly the figure of 1619.93 pF above is most likely too high to use in the real world. Having said that let's check our sums. We have 105 pF max and 10.5 pF min in parallel with 1619.93 pF which is the same as ( 105 + 1620 ) / (10.5 + 1620 ). This calculates out to 1.057977 : 1 which when applied to our tuning range would tune from 7.0 Mhz to 7.19999 Mhz or what we set out to do. Remember our strays earlier?. They would play havoc with this, so the 1620 pF would become in the real world 1000 pF + 560 pF + 100 pF trimmer ( i.e. 10 - 100 pF ).
I said earlier the 105 pF was possibly acceptable ***
Let's go back and reduce it to say 33 pF and redo our sums to get another Cpad value. Let me know your answer.
Some home brewers (hi-tech code word for building-it-yourself) advocate using a starting goal of 1 pF per wavelength of frequency. e.g. 7.0 Mhz = 40 metres (approx.) = 40 pF.
I must say I am not especially in love with that particular logic for many reasons which will become apparent as we become more deeply involved with filter and oscillator theory.
This is as far as I want to go on inductors and capacitors for the moment.
What is a Resistor
Resistance by technical definition "is the property of a material that determines the rate at which electrical energy is converted into heat energy for a given electrical current".
Mouthful?. Well look through the books I recommend to get a better insight. In particular if you don't already know Ohm's law backwards then learn it now!. It is as fundamental to your development as the first breath you took the moment you were born. Believe it.
It should be fairly obvious if you have managed to stay awake so far, that a resistor must exhibit some inductance. Depending on how it is mounted on a board or elsewhere then it will exhibit some capacitance also.
On a totally different tack, many people may not appreciate what is a cunning trick. In relatively low frequency circuits e.g. below 15 Mhz, surplus high value resistors make excellent stand-offs when building rat's nests. I use a heap of 1 Meg ohm or more resistors for this very purpose.
Of special interest to me is just what do you guys overseas use for resistors. Here in Australia our hobbyist suppliers (see Links) offer E24 2% metal film resistors for a reasonable price and I tend to use these. The 5% are becoming so small they usually become embedded in the feet of my grand-children. I would like to know what you use outside of N.Z., the U.S., Canada or U.K.
Now if we put two or more resistors in series (R1 and R2) then the total resistances will add together. If one were say 1K, or 1000 ohms and the other was 1K5 or 1500 ohms then the total is 2K5 or 2500 ohms.
On the other hand if we put two or more resistors in parallel (R1 and R2) then the total resistances will be less than the lowest value. If one were again say 1K, or 1000 ohms and the other was again 1K5 or 1500 ohms then the total net resistance is 600R or 600 ohms.
How is this so? Well because we have now provided two paths for the current flow and that means less overall resistance. The formula is:
(R1 X R2) / (R1 + R2) OR
(1000 X 1500) / (1000 + 1500)
Try it out for yourself on the calculator.